Bahas Soal Matematika   »   Matriks   ›  

Jika \( A = \begin{pmatrix} 2 & 3 \\ -1 & 1 \end{pmatrix} \), \(B\) memiliki invers, dan \( (AB^{-1})^{-1} = \begin{pmatrix} 1 & -1 \\ 3 & 0 \end{pmatrix} \) maka matriks \(B = \cdots \)

1. \( \begin{pmatrix} 4 & -1 \\ 6 & 1 \end{pmatrix} \)
2. \( \begin{pmatrix} 3 & 2 \\ 6 & 9 \end{pmatrix} \)
3. \( \begin{pmatrix} 2 & 0 \\ 0 & 1 \end{pmatrix} \)
4. \( \begin{pmatrix} 1 & 6 \\ 4 & 3 \end{pmatrix} \)
5. \( \begin{pmatrix} 4 & 5 \\ 6 & -5 \end{pmatrix} \)

(SBMPTN 2014)

Pembahasan:

Ingat bahwa sifat perkalian invers pada matriks berlaku: \( (AB)^{-1} = B^{-1} \cdot A^{-1} \) dan \( A^{-1} \cdot A = I \). Dengan demikian, kita peroleh hasil berikut:

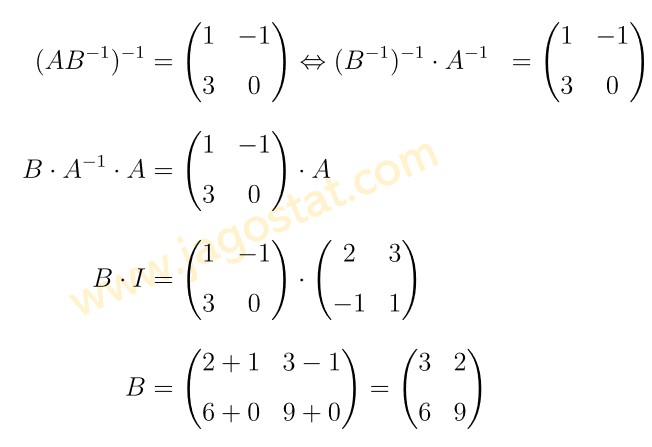
Jawaban B.